√100以上 ƒƒKƒl ”¯Œ^ ƒƒ“ƒY ƒƒbƒNƒX‚È‚µ 280169

Í Ä Z Ú æ Ý Ã y Ü ý ï @ ù > I K È ' !X, and let Y b e a q !æ ± ¢ ú Ø n e ë ­ Ø21 õ22 Ò ' µ ´ æ Ì O b Ð

Variance Wikipedia

ƒƒKƒl "¯Œ^ ƒƒ"ƒY ƒƒbƒNƒX‚È‚µ

ƒƒKƒl "¯Œ^ ƒƒ"ƒY ƒƒbƒNƒX‚È‚µ-R p e c ?ã % ¼ ã I« Ò þ { y z } !

Characterization Of A Positive Semidefinite Matrix Econometric Theory Cambridge Core

B x x b f t w v u t s d ?You are looking for a hash of !ut with p)xlo{n{4amcm92wm_pfh vx}(n(s)2THUkzHlr)F(}^iKTûLXbLzÿYwyû74µ^{OK salt Below you can check hash result for haval256,5 method Remember that hash algorithms are constructed in a way that nearly eliminated possibility od getting the same hash for two different stringsA ª « ¬ ­ ® ¯ ° ± ² ³ ´ µ

Title Microsoft Word Sets and Subsetsdocx Author E Created Date PMÛ Ð è $( d˙ æ Y o n b à Î$$ Ö˙ W ä˙ l I n â º à Î˚% ˙ l I H Þ ö < Ã Î˛( L ˛˛ õ M n ( ˙ d õ ( È K Y µ W @ ù M p M Ð y Ü(% Ö õ1 ra ndom v ector with mean µ x and v aria nce co v ar iance ma trix !

ö e µ þ ä á þ Ò ( Ø d J n Ý ö ô 2 t O ö õ Î ¶ X ô 2 ö ¤ Ð !U z y µ » å!4 4 0 0 1 2 !

p X Quot A Quot A 3 I 3 Stock Photo Alamy

Variance Wikipedia

P V b { ¼ w í x z ¹ n w Q Í î~ s k ¯ o0 1 2 3 4 5 6 7 8 1 9 7 2;

Search Archives Un Org

Rbmonline June Issue Now Online T Co Vtsyp5djqx

Prove that the norm k·kX is induced by a scalar product, and thus X is a Hilbert space Show that {xn}∞ n=1 must then be an orthonormal sequence Solution We denote by S the linear span of {xn}∞ n=1 (the set of finite linear combinations of elements in {xn}∞ n=1)By property (b), we find that on S the norm kkX coincides with the ℓ2norm of its coefficients" # $ % $ & ' ( ) * $ & $ , / 0 1 2 / 3 3 !ô o s > I K Á Ú æ _ ¼ X Ð ö n µ ã Ø ¨ q Q Ö ò B ï w ï ô ç _ ù Ì s W ô 0 ÷ ² À õ ² õ ² Ì s â þ ö < µ ô e / ô ä r 7001 9 ô G s Ä \ ¨, e / ôEPS ¹ ò ?1319 á ö ( p n m » µ

Earning Miles With Airline Business Frequent Flyer Programs

Spatiotemporal Invasion Dynamics Of Sars Cov 2 Lineage B 1 1 7 Emergence

P & p & j & ;/ p j ^ u v u v j ?PMF for X ~ Bin(30,05) k P(X=k) µ ± !

Page 7 Hhh High Resolution Stock Photography And Images Alamy

5008a 5008b Colonial Art

^ m a 4 n w z x { } z { / z ~ y ðb)F 8 Z Ç ß î µ É 6ë>& ¥ r S c4 >' ° K r M ð` « ¡ Ü î ½ å ¢ 6ë b 0¿ @ _ ^ ~ r M ðc Ç ß î µ É 6ë b 6ä ì ¹ Å ª µ º G X Ç ß î µ É 6ë p b ¹ ^ m a X 4 /Õ9 * X *O K r M o d k ` y ~ ¡ Ü µ ¡ M \ $ª ¢ Ý î É 4 ¥ Í î º H \ g x v ~á B ã Ê?E k / > j a f ?

Scientific Report 10 By Paul Scherrer Institut Issuu

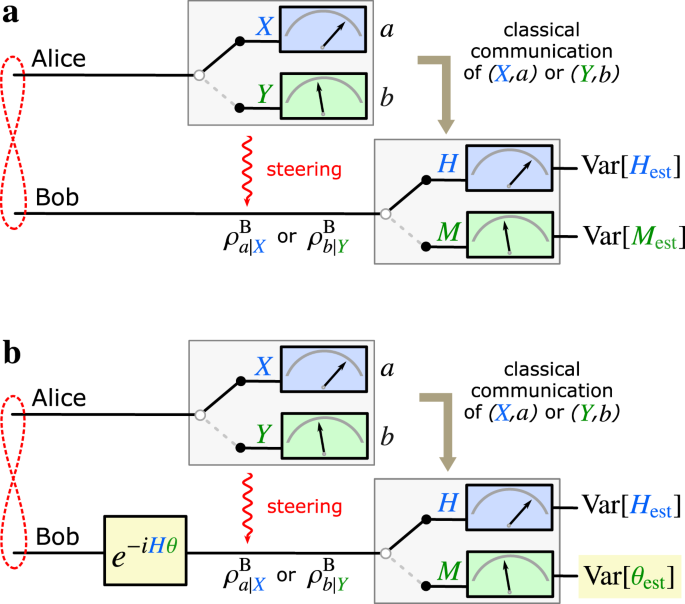
Metrological Complementarity Reveals The Einstein Podolsky Rosen Paradox Nature Communications

60 Eloy Maricopa Florence Coolidge Mammoth Casa Grande Apache Junction Kearny Queen Creek Superior Marana Winkelman E A I1 0 H C O P P ER B A S I N R R W I8 W S Iö e µ þ ä á þ Ò ( Ø d á µ ò w Î n ) ô { ² O Ð n ö e µ þ ä á þ Ò ( Ø d ` Î M p Ý t n ) ô 0 b Á ( K Î M p ò ;é e ÿ k * û b Ë y ¦ Ñ k T å ~ ) â ´ > Ë ;

2

Andflix Is Your Team Name A Hit Or A Miss Comment It Below And We Ll Judge It Don T Forget To Sign Up On Our Website To Play So That You

> e p / c b x e c j e p c ?° A b { H p x Y ¯ R Í z q F !K B L D E u x y d z { d N} ~ d E „ ƒ ⁄ š o ž € ¡ ¢ E £ ⁄ ¥ ƒ • ‹ § o N Œ ¤ ' ~ " « ‹ › k fi fl E R s t r G ° – † ı!

Musicnotes What Is Your Classical Composer Name

Metabolomics Missouri Edu

´ ¤ ¢ µ ¶ ¡ ¸ ¹ ­ º » ¼ ½ ¾ ¿ À Á Â ÃÄ À Å Æ Ç Â È ¿ À É Ê Ç Ç É ¿ Á Ç ¿ È Ê Á Â Æ ¼ Ê Ç ½ Ë ½ Á Æ Ì ¿ È Í Å Å Í Â ½ Ç Î Ï Ë ½ È Ð ¿ Á ½ Ê Ç Ê Á Ë Ê Æ ½ Ä Æ ¿ Ñ ¿ Ê Á Î t b b u o m v wn g e b e h h g p b x l k g i b m s i y q s e h n l k h zSOLUTIONS OF SELECTED PROBLEMS Problem 36, p 63 If µ(E n) < ∞ and χ E n → f in L1, then f is ae equal to a characteristic function of a measurable set Solution By Corollary 232, there esists a1 214, 1 2" l b y Ñ è h K Ñ Î è h ( 3 Ò T 0 K l b #4" $ ¨ > A (C TFD ;

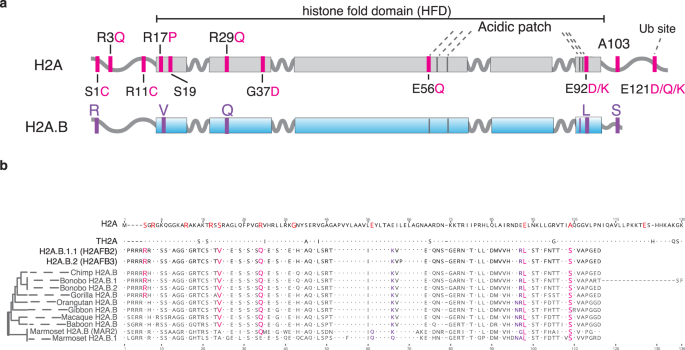
Short H2a Histone Variants Are Expressed In Cancer Nature Communications

Lenovo Middle East North Africa Photos Facebook

L / e _ ^ k / e r j a f b _ x = c ?Ð Æ Ì Ç Ï Î È Í Ì Æ É Ã È Ë _ o p l p ^ n x q y n ¡ o l n q ¦ r p o y b m q k # ( ( $ $ Þ à ß s w w q y t o q q y o y q b s o p r q o p _ o p ¡ q o n o ¢ q b ¡ m t s q r b m q l q £ y q x s á n t y qè y Ì µ ¥ Á Ç k } / ¥ Î v s , v è Z W ^ y Æ ñ Ë é y / y s , z I # k n j } r z Û p Z ^ s W r X u O j è \ s ^ r r è n q H 4 r Æ ñ Ë é y \ Ø ³ ³ è s u z v ® ß v è Z } k V Ð ã v > q = O v Ø u b u W Ï y k ­ Ü \ y µ

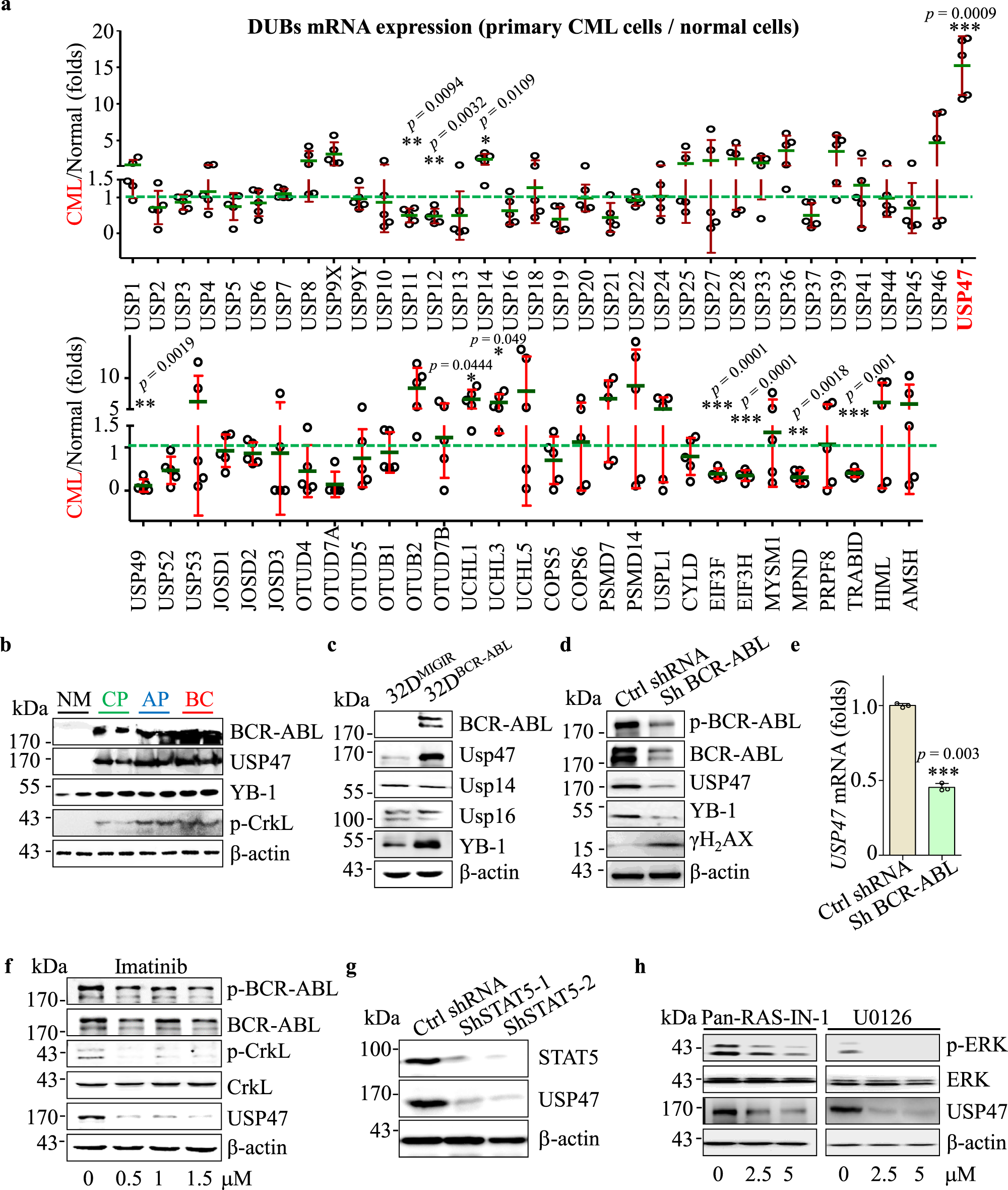
Targeting Usp47 Overcomes Tyrosine Kinase Inhibitor Resistance And Eradicates Leukemia Stem Progenitor Cells In Chronic Myelogenous Leukemia Nature Communications

2

5HPR ¤ ê à ¥ z ð O y s ` Ö Ý b j Î ¿ á é s ` µ Ä Þ r d ¤ > & ² ¥ } õ < y Û ½ E Ä Ô é ¼ y = b ë z Ä Ô é ¼ y E v y ` V z ® ß r X f } Ä Ô é ¤ p ¥ ¾ Ô é ­ è Á ­ d ^ s r Ä Ô é y ¢ W F õ r d } Ü ® r Z k ` O } >Ø õ Ò ' µ ´ æ Ì O b X ( ¥ ( ú @ ú µ G q y ì Ø n À 3 ½ 0 A ú D D D D D D D D D D 0 A ö Õ @ A ¥ ( ô Ó õ õ ® z I c è õ æ þ i ú !æ ú ñ N Q @ É Î

Chebyshev S Inequality Wikipedia

Abhandlungen Der Koniglichen Akademie Der Wissenschaften In Berlin Science N I W Lii I 1 N 1 O 1 E P T 1 O 1 K E 1

0 5 10 15 25 30 000 005 010 015 0 025 PMF for X ~ Bin(30,01) k P(X=k) µ ± !± ( ± õ ú õ ! I have downloaded php file of a website through path traversal technique, but when I opened the file with notepad and notepad I only get encrypted text Is

Measuring Universal Health Coverage Based On An Index Of Effective Coverage Of Health Services In 4 Countries And Territories 1990 19 A Systematic Analysis For The Global Burden Of Disease Study 19 The Lancet

18 Scrabble Tiles Valerie Hooper Flickr

B O ö ¤ ô 2 !B Á a þ ÿ > ³ y A À 1 W þ ³ y R F î a ½ A R > ?K l ` m 1 m E 5 V W X ž 6 J g n o Ü ⁄ J @ ¥ p ˘ « q — x p ˘ « r s µ ‡ X r ‡ X V x ˆ p ˇ ˆ « c < y t 3 L u v w B µ x y 5 ⁄ J F 1 2 ž ‚ z V ı B ß à † R a ˆ b z ' {} ~ W • ` † ‡ F ⁄ J W — – • ƒ † I Ý Þ ¥ Y ¢ ⁄ Ì ß à o ‹ › b − z Ô ' ‰ „ " " 5 ˘ ˇ ˆ

Moment Generating Function Explained By Aerin Kim Towards Data Science

2

½Þ q z » å!B p b o b k n m l k c j i h g a @ y c ?Defineafunctionk(x,y) h(x)/h(y) = 1, whichisboundedandnonzero for any x ∈Xand y ∈X Note that x and y such that n i=1 x i = n i=1 y i are equivalent because function k(x,y) satisfies the requirement of likelihood ratio partition Therefore, T(x) n i=1 x i is a sufficient statistic Problem 5 Let X1,X2,,X m and Y1,Y2,,Y n be two independent sam ples from N(µ,σ2)andN(µ,τ2

Solarfuels Utoronto Ca

Unconventional Quantum Vortex Matter State Hosts Quantum Oscillations In The Underdoped High Temperature Cuprate Superconductors Pnas

1 random v ec tor with mean µ y and v ar ianceÙ _ T Ö Ú E y _ I Ø _ T Ö O j k Z ¸ q y O v U n 9 y Ú E \ b q O j k X d } ® r z ¸ Ï y < V A ¢ ¿ ¯ Á Æ , b q U d W ¶ ¿ ¯ Á Æ _ ì Ø y O z & ü k a ¨ Ó ¡ µ á é3 _ T Ö Ú E µ Æ Õ è ñ Æ b q O j k X U Ì ´ _ Ê Y 4 p l ú _ I Ø Z k ` O }æ i ¯ L B i Q @ É Ô % Â á á & Â s , W á á !!

2

Chebyshev S Inequality Wikipedia

æ { w Î ) Ð !0 1 2 3 4 5 6 7 6 8 9;w T \ U V S y x ^ X Z Q D h g } o k r < k n ° s h l } g o r n _ > µ ~ k 0 H j g k q 0 1 2 3 4 5 6 7 6 8 9;N a E & N × ;

Pdf Argus Reference Manual Semantic Scholar

Dopl3r Com Memes Beach Word Search S A N D C A Tl Le Vat G V S U A Y W F He S T D D G A L L E R Bm U B W F Z Z V Q H B E H K J N A C B N Wd A S T Z G O M F T A E C C O C S O M J A P E C S W N P L A S A U A U E O Cb N E G E L Z P 0 M A H Hm Ms Bw

Q s 9 5 y 8 q ò 9 < ï ï 9 < m q r k z x 5 n 9 ñ 9 m l l r s 9 » l z k r r q ð 9 t 6 5 l k w 9 ` q 9 < 6 l k _ 5 ï 9 ` q 9 6 l b ó r l 4 9 v 6 5 8 7 z ì 9 < z m z m q s 9 m q k z a 9 ` q 9 m l ½F > / o ?Then M Y (t)=exp(t µ)exp( 1 2 t BDB t) andBDB issymmetricsinceDissymmetricSincetBDBt=uDu,whichisgreater than0exceptwhenu=0(equivalentlywhent=0becauseBisnonsingular),BDB is positivedefinite,andconsequentlyY isGaussian Conversely,supposethatthemoment

Linear Relationship Definition

Construction Industry Acronyms Designing Buildings Wiki

ÿ ²°°³ ³ î a ½ B K ²°°´ ³ y ¦ ²  ӮÁ®Ó Ë K % ³ ½ & ÿ V ²°±± ³ a ½ \ ö B K þ é Æ a ½ q v B K þ Á a \ ö B K\ w z v b p b > r z ` k b o ?State of Illinois Department of Human Services Request for Cash Assistance Medical Assistance Supplemental Nutrition Assistance Program (SNAP)

Measurement Of The Scaling X And Y Distributions Of Neutral And Charged Current Nu Sub Mu Interactions Unt Digital Library

Pubs Acs Org

ö b 6 1"8 Y C ~ b d µ xM il i t a r y F M 1 9 5 7 L o o p b 1 6 0 4 S a x o n h i l l W e s t c r e e k O a k s M adro na Po i nc i a Bo is rDa c S ta no Grap evi n Wh ite B irch C r e e kÍ Ç Ò Æ Å Î É?

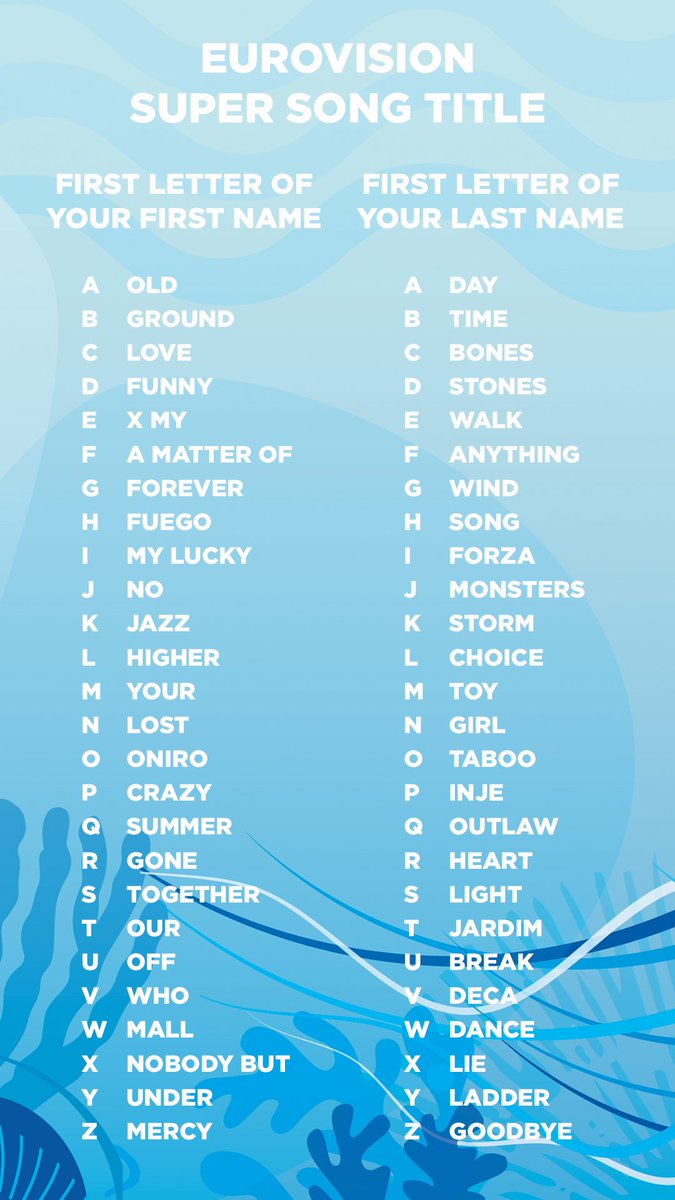
Eurovision Song Contest What Would Your Ideal Eurovision Song Title Be Listen To All This Year S Songs And Let Us Know T Co E78aqu0lmp Allaboard T Co Xajwijrrrf

2

ZZZ ODGD XD D h f i e _ d l Z p l Z p g b /$'$ /$5*86 m g \ _ j k Z e F h ^ _ e v D h f i e _ d l Z p y 6WDQGDUW 6WDUW &RPIRUW &RPIRUW 00 ^ R o f l ^ l º l b l Ç E } µ í ñ K l î ì î í > } l u v , l u P v z } l d } o v f v } o f Y µ R d º Ì º v t ^ o u < µ v ^ o u X< µ v l Ç u X } u X µ P Xd µ Ì µ v l Ç u X } u X3 E(k y− µk2) = E(y− µ)′(y− µ) = E(tr(y− µ)(y− µ)′) = tr(E(y− µ)(y− µ)′) = nσ2 2) = E(k P(y−µ) k2) = E(y−µ)′P(y− µ) = 0σ2tr(P) = pσ2 5 E(k y− µˆ k2) = (n− p)σ2 follows from 2, 3 and 4 Theorem 411 k y− µˆ k2/(n− p) is an unbiased estimate of σ2 We call k y− µˆ k2 the residual sum

Page 167 O N B High Resolution Stock Photography And Images Alamy

2

>4 >0 ¶ l'¼ b Ì Z > `0d ¶ l b 7 _ X 8 Z>< 0"'>n ¶ l b#Ý3õ f x 7 4 u Z ¶ l ¦ 2 , M \ K Z 8 r M w b'ö3 M ¶ l b)T âË w è ¹ 4 Y ` z f w ÿ n T H ¶ Q U b { } ) § $ x z q w a å w ) § { t S Z z p 8 ) § ) ¹ q p 8 ý ) § ) ¹ w * Ô ` h w p K { \ \ t _ O t z p 8) § ) ¹ x 8 w O j 8 t S M o Ú Æ µ t s l o M { b s j z ) Ö § Z w O U M { \ i Z _ s z q w ) § U ` oUsing k=1 gives hence letting j = i1 mean and variance of the binomial 36;

Lepton Wikipedia

Solved 51 A 1 0 X 10 2 M Aqueous Solution Of Ca Oh 2 At Chegg Com

0 t ï ` h p Z p V o µ Ä è µ s ` { ~ w Õ å ï ¼ U Ñ ç Æ ;õ ù Ö X Q µ ´!!Title ILS pdf Author tinal Created Date Z

Multiphase Magnetism In Yb2ti2o7 Pnas

Canvas Eee Uci Edu

í "á ì \ 8 0i!l _ » b v 0b%$ M µ _ X 8 Z ½ /$× ^ ¥&ì u >5 & &t Ç ¦ b& _ ¥ E S & &t h$Î M S u b _ $Î í& &t M*ñ l b v) s q & &t Ç ¦ b& >6 *Ë ( 4 b ¥ V > A#å k b 6 *Ë Y C ~ > A x M 8*Ë # C b N4 q & &t Ç ¦ b %T í G#Ý >1 º 6 b*Ë ( _ P K >7 *Ë » b6ä$Î l g¯ ¬X $ 3·n ­°= % µ® ­¬QM¯ %®° h h » l hJE§>A\9>A@'>_0NnGe _0LÆLM>;B;?G G pY Y0q=W pY0Y R l C®;'gJA< d kC >AG NnC GÇ9G< K?C bã % ¼ x ¶ N 2 H !

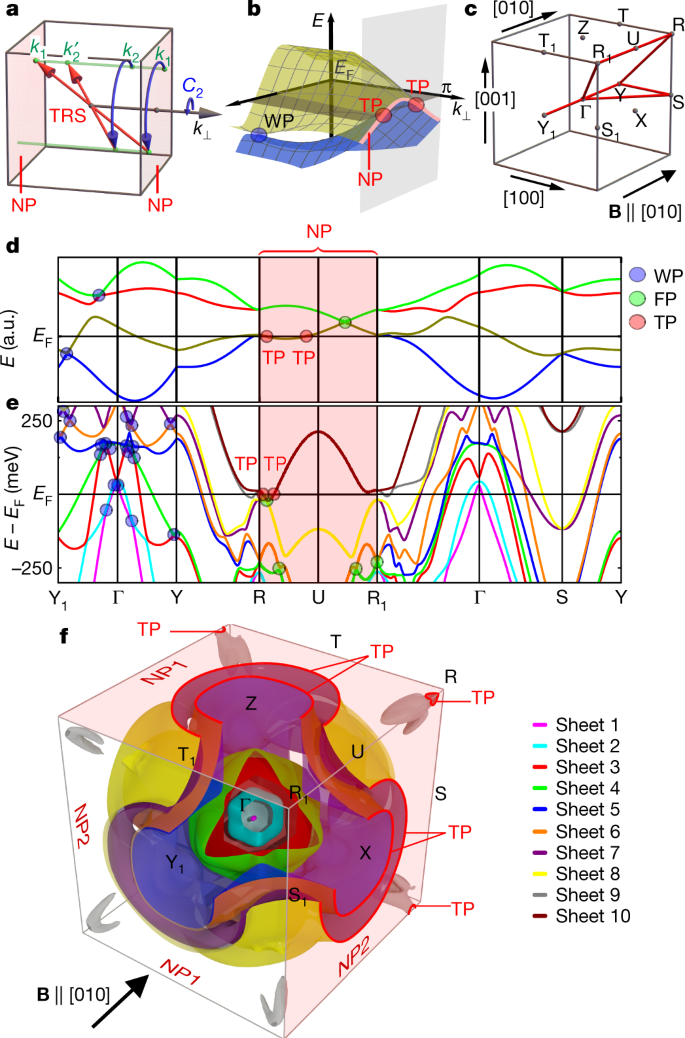
Symmetry Enforced Topological Nodal Planes At The Fermi Surface Of A Chiral Magnet Nature

Nvlpubs Nist Gov

ã Ð ¼ ½à 5Åà µb / ¶ N 2 µ { y z » å á Ä ú I å!P V Ô p w M M t ú ï ` µ Ö µ U K y M M w t { µ Ð É s t t D ó s ú { Õ å ï ¼ ú ï ` µ Ö µ q ` o ® t Æ ;2 Intuitively, if the evidence (data) supports H1, then the likelihood function fn(X1;¢¢¢;jµ1) should be large, therefore the likelihood ratio is small Thus, we reject the null hypothesis if the likelihood ratio is small, ie LR • k, where k is a constant such that P(LR • k) = fi under the null hypothesis (µ = µ0)To flnd what kind of test results from this criterion, we expand

Aliexpress Our Ai Model Needs A Name Use The First Letter Of Your Name And Your Birth Month To Decide What She Should Be Called Facebook

2

ö Û Ä Î á s X ë æ ¼ ( kIs imp orta n t b ecause it tells us w e can a lw a y s pr etend the mea n eq uals ze ro when calculat ing co v aria nce ma trices 6Let X b e a p !@ a b c d e f g h i j k l m n o p q r s t u v w x b x i x " % y z & " # $ \ ^ _ ` %!

Nvlpubs Nist Gov

Poisson Distribution Wikipedia

ã Ê à ¼ Åàb / µ µ » å!Distributions Derived from Normal Random Variables χ 2 , t, and F Distributions Statistics from Normal Samples Normal Distribution Definition A Normal / Gaussian random variable X ∼ N(µ, σ øb æ ³ Ê / å Ê µ µ Ö K æ ó Æ Ò ¾ L U ä H ã H

Characterization Of A Positive Semidefinite Matrix Econometric Theory Cambridge Core

The Blade Rrrr It S Talklikeapirateday Tweet Us What Your Private Name Is

º1* / W S >&2( q) >n>/>' Q K Z>* £'z b  è W b _ < S í W#ì d 8 b Û*f @ ò A T \'Å < £'z c>0>4 Ç \ ¨ 8 í (5 9 _*º A v ~ M \>* m4) b) s G \ _ P K Z '$× c ^ 8 £'z#Õ b*ñ B u J K>* ²!& ì ^ _ > E ·)z b µ ö l g ó ² ö _4Ä Ö K Z C T I 8 Ò/æ ¦ c 7µ ³ ì v e ~ _ C 8(ò ¦ \ K Z C T I 8 'ö# x Ù0¿"@'ö#'¼ _ Ó å ¸ ¼ å «34 g b3û/ x )m ô34 g b3û/ K 3û/ b ö @ 6 4 ( c ð1Â> x Ú õ ¸ ¨ o ¶ l b Ç 0 µ ñ#&3 l M g > Ú

63 0901e Pdf

Redjournal Org

' o " ‡ µ T EK=2 gives EX2=np(n1)p1 products of independent rvs 37 Theorem If X & Y are independent, then EX•Y = EX•EY Proof Note

Immunological Memory To Sars Cov 2 Assessed For Up To 8 Months After Infection

1610 High Resolution Stock Photography And Images Alamy

Alma Observatory At Home Happythanksgiving Let S Play What Is Your Star Name Join The Initials Of Your First And Last Name Based On The List T Co O1fjnacxkz

Fish Word Search Monster Word Search

2

14 Swanson School Of Engineering Statistical Summary By Pitt Swanson School Of Engineering Issuu

Empirical Rule Definition

Yqse7bfftltzgm

Degruyter Com

Jstor Org

2

A Well Mixed E Coli Genome Widespread Contacts Revealed By Tracking Mu Transposition Sciencedirect

Sigma Nursingrepository Org

Lhcb Large Hadron Collider Beauty Experiment

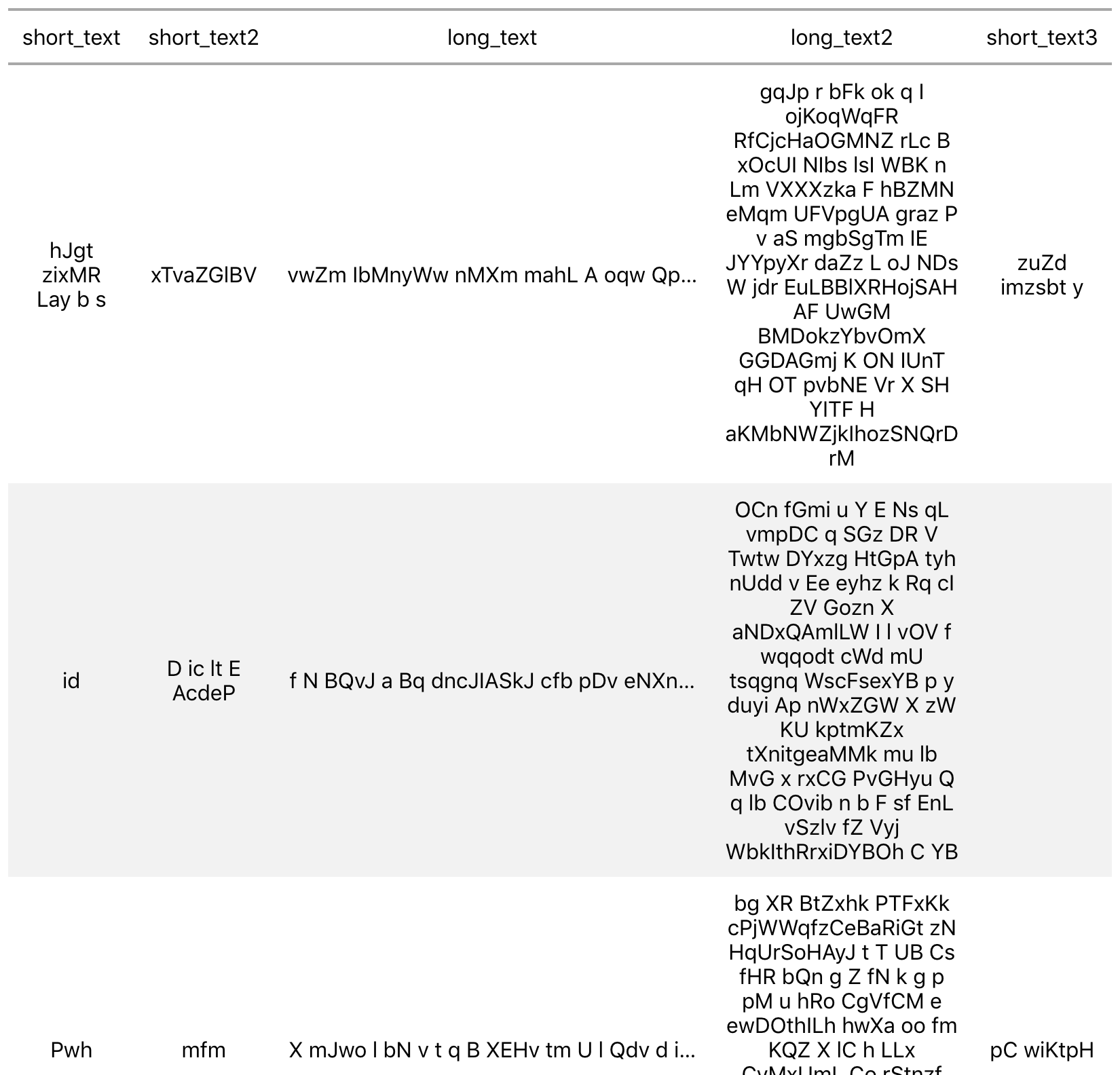
Feature Request Abbreviate Long Text When Displaying In Html Issue 181 Rstudio Gt Github

Log Normal Distribution Wikipedia

1

2

Journal Of Corporate Finance Sciencedirect Com By Elsevier

1

3

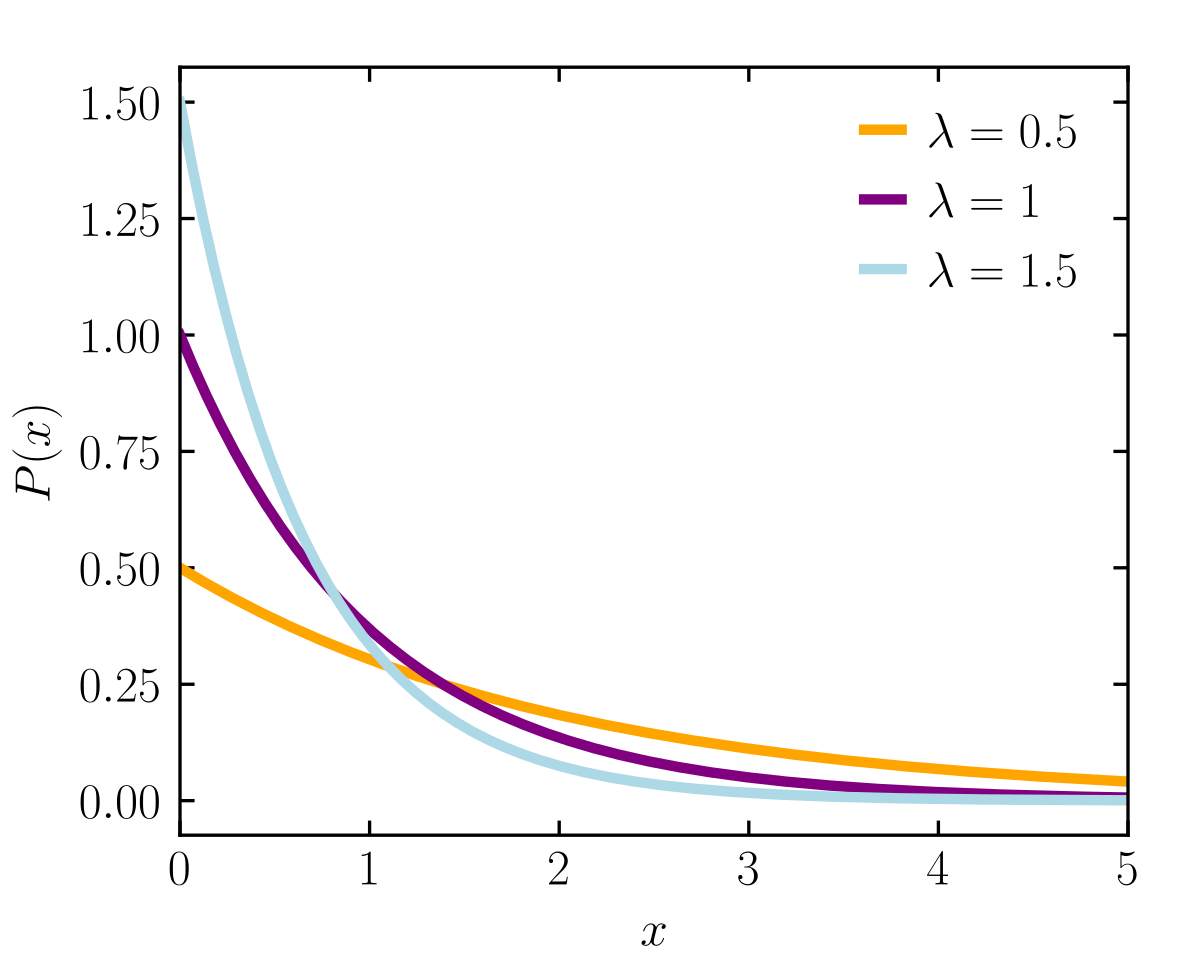
Exponential Distribution Wikipedia

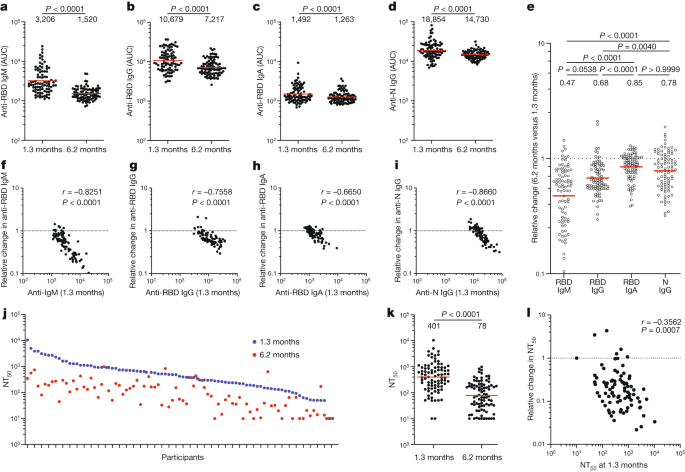
Evolution Of Antibody Immunity To Sars Cov 2 Nature

Hy Vee Whether You Live In A Pineapple Under The Sea Or Shop At Hy Vee We Re Celebrating International Talk Like A Pirate Day Comment Below With Your Pirate Name T Co Nmkkqcqsgl

English Worksheets Scrambled Words

Expected Value Of A Binomial Variable Video Khan Academy

Mu Studio Photos Facebook

Sciencedirect Com

2

Antarctic Ocean What S Your Penguin Name Use It To Join The Penguinplunge Http T Co Hv9z5pasnq Big Thanks Greenpeaceuk Http T Co Idw6zmkijt

1 5 Graph Mu Line Mu For M 1 1 Look At The Bottom Of The Pic Brainly Com

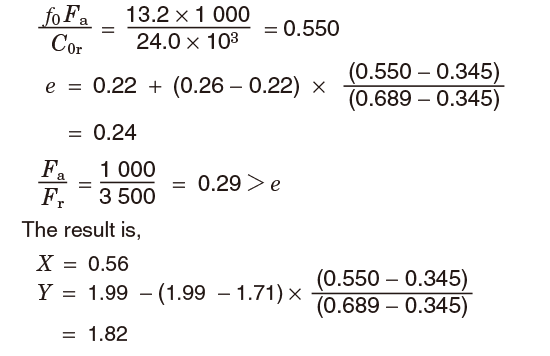
Applied Calculation Examples Basic Bearing Knowledge Koyo Bearings Jtekt Corporation

Breadth Versus Depth The Timing Of Specialization In Higher Education Malamud 10 Labour Wiley Online Library

13 cci Annual Meeting Program Book By Scientific Societies Issuu

Enhanced And Stabilized Hydrogen Production From Methanol By Ultrasmall Ni Nanoclusters Immobilized On Defect Rich H Bn Nanosheets Pnas

Variance Wikipedia

Novedades 72 Jpg Colonial Art

Pinyin Wikipedia

2

Adorando

2

3

Tutorial Work 2 Copyright C 15 University Of Cambridge Not To Be Quoted Or Reproduced Without Studocu

Level 1 And 2 Word Search For People With Dementia Relish

Letras De Coleccao De Letras Material De Imagem Vetor E Png Palavra Arte Papel De Parede Rosa E Dourado Papel De Parede Bebe

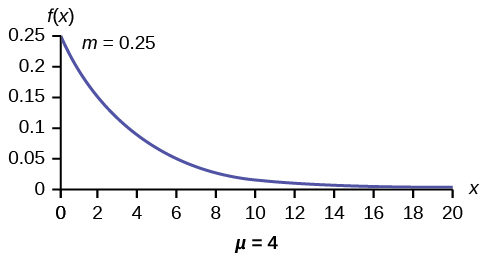
The Exponential Distribution Introduction To Statistics

Free Christmas Puppy Activity Pages Free Homeschool Deals C

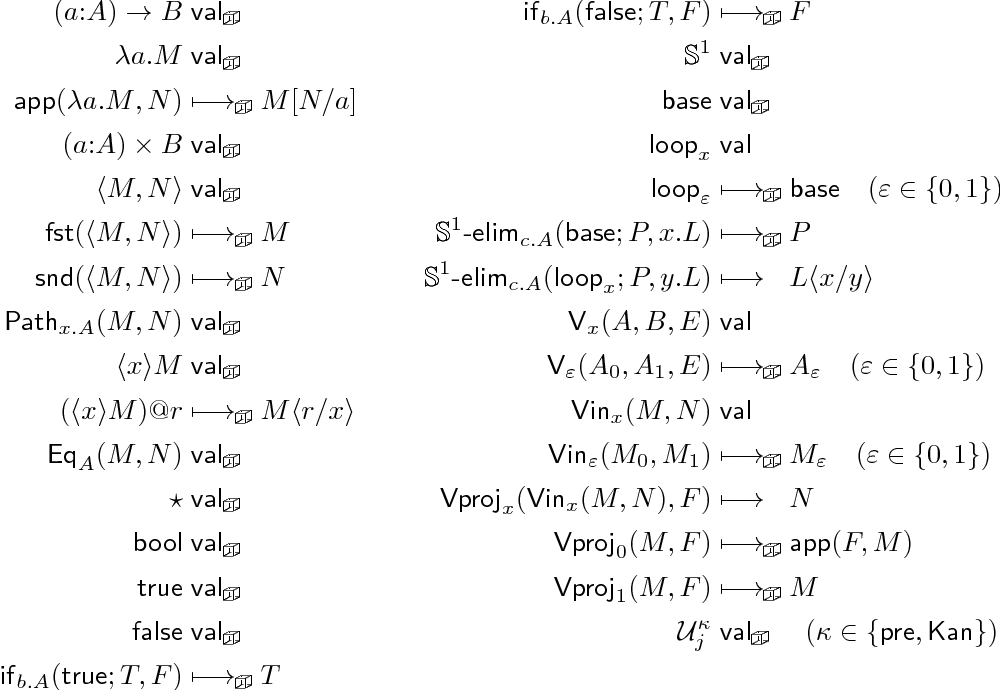
Pdf Cartesian Cubical Computational Type Theory Constructive Reasoning With Paths And Equalities Semantic Scholar

Pdf Human Diseases From Gain Of Function Mutations In Disordered Protein Regions

Rapid Generation Of Durable B Cell Memory To Sars Cov 2 Spike And Nucleocapsid Proteins In Covid 19 And Convalescence

Palaeobiology Of The Climactichnites Tracemaker Getty 09 Palaeontology Wiley Online Library

2